News (and not so news)
26 November 2023 It's the EU's fault. Not!
Apparently, the company Booking.com (BKNG) considers their customers' bank accounts as a resource from which they can freely draw. And they seem to have replaced all humans in their call centers with a sleazy chatbot.
When traveling Morocco last year, we used their service a couple of times. Unfortunately, when they bill your credit card, there is no indication whatsoever about the accommodation name and location. Not even a check-in date. And no confirmation number. (I would have thought these guys have computers!) The only thing you see is the price they charge for the stay. With some luck, you can log in to their site and find that price in the “Bookings & Trips” overview.
After returning from Morocco, they had charged me 67,32€ from my credit card for a stay I could not match with any of our stays in the “Bookings & Trips” overview. I searched their web site for a phone number but could not find any. Their FAQ was useless. Somewhere hidden, I found an email address. I wrote them asking for clarification. This was their reply:
We would be happy to help you with your booking, but first we need some additional information from you.
Please reply to this message providing as many details as possible, including:
• Confirmation number:
• PIN number:
• Name of the main guest:
• Email address (used to make the reservation):
We are looking forward to your response.
--
Angeline C.
Booking.com Customer Service Team
How brilliant! Except for my name and email address (seriously?), wasn't this exactly the information I was asking them for? I replied, reminding them of my name and email address, and explained the situation again. Guess what – I got the same reply again, but this time signed by Rochelle V. I replied again; same reply but from Kyla S. Is it Groundhog Day? Weren't they reading the thread? Or was this email produced by some stupid AI chatbot, crafted to fob me off? After three more such emails, my tone got slightly demanding: “If you are an AI, please forward this to a human.” Then, a new reply:
You've recently contacted us about a charge of 67,32€. After a thorough check, we've found that the reservation which originated that charge has not been connected to any suspicious activity. Unfortunately, we are unable to share further details due to GDPR.
If you still believe this charge is incorrect, we kindly recommend you to dispute it with your bank or card operator. They will be able to guide you further.
Kind regards,
--
Booking.com Customer Service Team
What a derisive reply! They are my business partner. My bank is merely an intermediary. And they seriously say that the European GDPR doesn't allow them to justify their grabbing my money? This is plain fraud! I replied again, only to get the original silly email asking for my name, email address, PIN, and confirmation number. This time signed Sohila M. This went on four more times. I eventually got tired of this and contacted my credit card company…
Dear Booking.com, if your corporate IT is a trainwreck, when it charges phantom amounts from your customers' cards, then you shouldn't replace good human service staff with the most imbecile and incoherent parroting AI chatbot! And, please, spare us the lame excuse that a EU regulation is the culprit for your deplorable corporate incompetence. -- Richard K.
Update (16 March 2024):
Three months later, the
credit card company paid the money back. With no comment whatsoever. I
guess they got tangled up in an infantile AI chatbot.
18 November 2018
Why I left Facebook. (tl;dr: Facebook betrays their users' trust by offering anything it knows about their inclinations to well-paying economic and political parties. These, in turn, microtarget their ads on Facebook so to appeal the recipients. The absence of witnesses eliminates all checks for trustworthiness.)
Update (30 Mai 2025):
I also left WhatsApp –
and I feel really good about it. It is
the
wrong technology
in the
wrong hands. (Facebook and WhatsApp are both owned by Meta.)
Update (2 September 2025):
I also left
LinkedIn – and I feel really good about it. It did not like me. After
signing up in May, I ran into a weird technical problem with their Persona
service (for passport-based identification): I ended up in a kafkaesque
infinite loop of “Verify with Persona”, “You've already
submitted a request. Please try again later.”, repeat. I was
effectively logged out from my account. I then discovered that a) you need
to be logged in to write tickets, b) the contact interface is served by a
brainless AI, c) their FAQ does not explain how to leave LinkedIn, d)
registered letters to LinkedIn Ireland, Wilton Place, Dublin 2 are not
answered, e) the Irish Data Protection Commission does not reply to requests
to get personal data held by LinkedIn deleted... Today, I miraculously could
log in again and used the opportunity to delete my data and leave LinkedIn
for good. Don't bother to ask for my LinkedIn profile.
Update (3 November 2025):
I also left
Instagram – and I feel really good about it. I am nauseated by all the fake
AI images, by the endless stream of ads, by the bubble's besetting reality
distortion. (As Ezra Klein wrote about social media: “We are shattered
inside the algorithm, the shards of us sent flying into the world. Instead
of being complex to one another, we become incomprehensible, almost
unimaginable, to one another.”)
19 December 2011
While attending Sage Days 24 last year in July at RISC (in arguable proximity to Linz, Austria), I stumbled across a trove of bugs in various software projects. They all revolve about branch cuts of complex functions like log x, sqrt x, asin x, etc. Branch cuts are curves in the complex plane across which such functions are discontinuous. Huh? The issue is that an arbitrary choice must be made in order to make these functions unique (i.e. single-valued). For example, the complex logarithm is commonly defined as log x = log |x| + i arg x and there we already see it, since arg π/2 = arg 5π/2 = arg 9π/2, etc. To resolve this multi-valuedness (and make the logarithm a well-defined function), one has to commit on one choice. For the logarithm, that choice is arg x ∈ ]−π…π]. So we have a branch cut along the negative real axis: while crossing from just below to just above it, the logarithm picks up a 2πi. Similar for other functions.
It is important to keep in mind that the branch cuts are completely artificial and their positions are nothing but a human-made convention. They have to be somewhere, but where exactly is a matter of choice. Still, it is quite important that the implementors of software packages make the same choice simply because debugging branch cut conventions is beyond most hackers. Abromowitz and Stegun made some choices long ago. When computer packages came up, people tried to standardize these so to avoid Babylonian confusion. The signed zero in many floating-point implementations required us to think even more about continuity on those branch cuts. Language standards like those for Common Lisp and C99 followed each other since long. So, I thought the world was a safe place...
But at Sage Days 24 it turned out that these standards were widely violated! Many widely-used software packages gave completely different results for inverse trigonometric and hyperbolic functions. This surfaced in Sage [bug #9620] because it is an umbrella for many of these packages. Even one of the most venerable, respected and used packages, PARI/GP, got many of them wrong [bug #1084]. GCC had a fallback implementation in its libstdc++ with unconventional acosh [bug #50880]. GSL completely failed to honor zero's sign at branch cuts of sqrt, asin, acos, atan, although it supports signed zero. I sent them a patch.
But the upshot is that some people tried to standardize those branch cuts in the LIA-3 standard [ISO/IEC 10967-3] once and for all but made them inconsistent: The convention from Lisp, C, and C++ for systems that do not support signed zero is to “map a cut so the function is continuous as the cut is approached coming around the finite endpoint of the cut in a counter clock-wise direction”. The branch cut of the complex acosh function runs from +1 to −∞, so the function should be continuous with the upper half plane. But LIA-3 effectively specifies the branch cut of the complex acosh function to be continuous with quadrant II between −∞ and 0 and continuous with quadrant IV (not quadrant I!) between 0 and +1 while claiming that it “fits both with Common Lisp and C99 requirements when zeros don't have a distinguishable sign”. Inconsistent. Ouch.
Let's all respect branch cuts and keep the world a safe place!
Update (28 May 2012):
Prof. James Davenport
confirmed the bug in the LIA-3 standard. He says he'll try to get an
appropriate correction affixed through Malcolm Cohen from NAG. But this may
be difficult. At the moment, it is unclear anyway if anyone cares about the
standard. No ISO/IEC language has actually adopted it.
19 January 2008 decimal(γ) =~ "0.57721566[0-9]{1001262760}39288477"
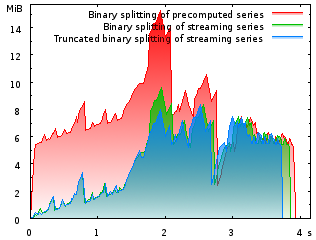 |
Memory footprint when computing and printing π to one
million decimal digits as a function of runtime in seconds. Here, the savings
are mainly due to the computation of the rational terms on demand (i.e. “streamed”). |
Today, I finally released CLN 1.2.0. This work was started with a branch in the CVS tree in December 2005 when, after attending the Many Digits Friendly Competition in Nijmegen, I got the wild idea of using CLN to crunch some huge numbers with hundreds of millions of decimal digits. The problem was that CLN had never been used for such huge numbers, and quite a few types were too small for this: counters were mere 32 bit integers, floating-point exponents were 32 bit, etc. The 32-bit exponent types turned out to be the most immediate barrier. This is because, just like in IEEE 754 arithmetic, floats in CLN have a biased exponent and an integer mantissa of a given size. Now obviously, if the mantissa's size becomes larger (higher accuracy) but the magnitude to be represented is fixed (say 3.1415926…), the exponent will have to become smaller and smaller in order to compensate that larger integer mantissa. Since the implicit base is two, 32-bit exponents basically limit modest floating-point values to 231log(2)/log(10)≈646 million decimal digits accuracy. This doesn't seem to be entirely esoteric, as it has actually been reported as Debian Bug #310385.
Together with Bruno Haible, all that was changed. As a result, it should've been possible to compute π=3.1415926… to one billion digits. At least in theory. This, however, turned out to consume much more memory than I expected. The first reason for this was found rather quickly: The rational number approximation of π was computed by first computing N terms of a series of rational coefficients (the one that was used by the Chudnovskys) and then by applying the binary splitting algorithm to evaluate the series efficiently. But the original series was kept in memory during all this time and released only after the final division when the rational number was converted into a floating-point number! However, the machinery for computing the series terms on demand during the binary splitting procedure was already there. Using it, the peak memory consumption was reduced by one third (green curve).
For CLN-1.2.0, I applied the same technique to other constants as well, and even to some trigonometric functions. However, memory footprint was still obscenely high in some cases. This is where a second crucial observation steps in: When computing the series approximation for an irrational number, the numerators and the denominators of the coefficients usually grow in a polynomial fashion. That is, their integer length grows very slowly, sublinearly. Binary splitting splits the sum into two halves and these again into quarters and so on and computes the sum while pushing part of the complexity of the computation from the sum into few big multiplications – which is a win when multiplication is asymptotically faster than O(N2). However, some of the resulting integer coefficients become quite large, much larger than the desired result. But this is a waste of memory: If an intermediate integer has 10 million digits, but the final result is supposed to have only 1 million digits, rewriting the intermediate integer as a floating-point value with 1 million decimal digits precision only will not alter the final result! This way, the excess digits are essentially compressed into the floating-point's exponent. Almost all constants in CLN-1.2 take credit of this kind of savings by coercing all integers to floating-point numbers as soon as the integer length exceeds the length of the desired result's mantissa (blue curve).
 |
Memory footprint in MiB when computing and printing the
Euler-Mascheroni constant γ to one million decimal digits, as a function of
runtime in seconds. The savings due to early truncation of integers are
dramatic. Indirectly, it even reduces the runtime. |
One potential problem with this approach is the introduction of new roundoff errors. In theory, chopping off precision early may poison the final result – although only slightly so, because it only occurs on the top few levels of a binary tree. For this reason, the rewritten functions in CLN were carefully tested before the release. I haven't observed any deviation from the old results while doing so. No more guard digits had to be introduced. (If you see a theoretical reason why this should be so, please let me know. Also, please do drop me a note if you know of some prior art. I haven't found any mention of this technique in the literature — only occasional statements about binary splitting being impractical for some series due to its memory requirements. But that is incorrect, if one takes truncation into account!)
The new techniques turned out to be most effective with the Euler-Mascheroni constant γ=0.5772156… (second graph). Computing one billion decimal digits would have consumed the prohibitive amount of ca. 500 GiB memory with CLN 1.1.x. Although the algorithm is unchanged, combining the two techniques described above, it is possible with about 20 GiB using an off-the-shelf CLN-1.2.0 library. According to Wikipedia and Xavier Gourdon's list, this establishes a new world record. At the very least, it is finally a high-precision computation of a mathematical constant where the program is completely open-sourced and not some black box! The computation and simultaneous verification with some more digits on another computer each took about one week on 2.6 GHz Opteron machines running Linux. No attempt was made to parallelize the program. Both computations completed in the wee hours of January 1 2008 and the first 116 million digits do agree with Alexander J. Yee's previous world record. If you make another computation, you may wish to check your result against mine. Here are all the decimal digits for download:
| Digits | File | |||
|---|---|---|---|---|
| 1 | – | 99999999 | euler.100m.bz2 | |
| 100000000 | – | 199999999 | euler.200m.bz2 | |
| 200000000 | – | 299999999 | euler.300m.bz2 | |
| 300000000 | – | 399999999 | euler.400m.bz2 | |
| 400000000 | – | 499999999 | euler.500m.bz2 | |
| 500000000 | – | 599999999 | euler.600m.bz2 | |
| 600000000 | – | 699999999 | euler.700m.bz2 | |
| 700000000 | – | 799999999 | euler.800m.bz2 | |
| 800000000 | – | 899999999 | euler.900m.bz2 | |
| 900000000 | – | 1001262779 | euler.1000m.bz2 | |
Update (31 January 2008):
A Wikipedia
edit has brought to my attention the website of Shigeru
Kondo. It turns out that he already computed 5 billion decimal digits of γ
last year. His computation agrees with mine as far as that one goes. Funny, the Wayback
Machine indicates that he already had computed 2 billion digits in July
2006, twenty weeks before Alexander J. Yee
claimed the world record with 116 million digits. Okay, Xavier Gourdon's pages
are no longer a useful reference.
Update (10 March 2008):
Today, Paul Zimmermann sent an email and
points out that the truncation method has been mentioned before in a
paper by Xavier Gourdon and Pascal Sebah. On page 4, these authors state
this “crucial remark for practical implementations” after having talked
about “treatment for large integers with limited precision”. (I prefer
the term “floating-point with arbitrary number of digits”.)
14 December 2007
Natan entwickelt derzeit Fähigkeiten, die eine Laufbahn als Lokalpolitiker vorwegahnen lassen: Er hat es innerhalb von nur drei Wochen dreimal in die Zeitung geschafft. Sonst sind es meist Landräte, Bürgermeister und Dezernenten, die sich so medieneffizient zu positionieren verstehen. Woher er das nur hat. :-/
9 November 2007
This year marked the 25th anniversary of the Dutch Unix User Group – reason enough to celebrate. And so they invited some celebrity speakers and organized a conference consisting entirely of keynote speeches. It started with Andrew Tanenbaum speculating about the next 25 years of computing. Bjarne Stroustrup explained the C++ standardization process. David Korn (the “k” in ksh) elucidated how to make sense of Windows systems. Amazon's CTO Werner Vogels widened our perspective on his employer as deliverer of toilet paper (check out their reviews!) and provider of an electronic marketplace platform. In a fervent speech, Whitfield Diffie sparked candid optimism regarding the longevity of present-day cryptosystems. To emphasize the state occasion, the crowd was not hosted in some univerity's auditorium but in Amsterdam's elegant Beurs van Berlage.
Now, several thoughts are spinning in my head and there is one that I'ld like to share: The energy consumption of all those computing devices should not rise any more! Andrew Tanenbaum is optimistic that “the guys at Intel have really understood it” and will even bring the energy consumption down. Although I wish he was right I didn't quite agree and objected that the cumulative energy consumption of all computers (embedded, PCs, routers, etc.) has only been rising during the last decades. Sure, the power consumed by individual computers cannot rise any more because the dissipation of heat is becoming an obstacle. In 1993, when Intel introduced the Pentium, people were ridiculing it's thermal problems due to the ineffectiveness dissipating 5 W at a time where DEC was successfully dissipating 15 W consumed by the Alpha processors. But present day CPUs run at 100 W and their surface power density exceeds that of fuel rods inside nuclear reactors! This cannot increase much. But their number will! The OLPC XO has 2-3 W total power consumption and in most cases will not be powered off the grid. We may also remove billions of future wearable devices from the bill since their need to stay independent of the grid will drive manufacturers to scavenge ambient energy. But what about gamers' devices, office PCs, and internet routers? Their number will surely continue rising as will the number of circuits on each of them. The trend is to put more computing cores on one chip and this will certainly make programming more challenging. But I am sure the ingenuity of hackers will adapt to this new environment – it is certainly easy to parallelize a computer game's rendering and physics engine or a router's traffic shoveling. So, I'ld say that the average high-end device in 20 years will be as hungry for power as today's. How many devices will there be? Well, Gardner says that 1 billion PCs were shipped in the last 25 years and the same number will be shipped in the next 5 years. Based on this I make my bet: Twentyfive years from now (in 2033) the world's computers will consume 25 GW of power, the equivalent of 20 large thermal power stations. Let's see…
Update (28 November 2018):
Reality tops my
prediction from 11 years ago by far. Most likely, the world's computers already
consume more than 25 GW of electric power. We may be using efficient mobile
phones for much of what we do in terms of computing. But the data centers
behind that technology already consume an
estimated
20 GW! One may wonder if the “guys at Intel” are to blame, or
rather online shopping, crypto mining, and our sharing of cat
pictures. :-(
13 September 2007 Publish and Perish!
Recently, publishers attempting to railroad the open access model of scholarly material have gained some media attention. Ultimately, it is the diminishing of the publishers' reputation that reduces their revenues and thus lies at the root of their reactionary activities. The traditional publishing system started to corrode in the early 1990s with the advent of the WWW when scientists started publishing their preprints on arXiv.org and similar servers. Face it: Nobody really needs a printed paper when it is easy to download the articles from the internet.
One point I haven't seen being raised in the recent brouhaha is the publishers' outstanding contribution to their own demise. I think they could have easily capitalized on the volatility of web links by providing a safe heaven for digital articles. Permanent availability of online articles ought to be one of the weak points of non-professional publishing efforts. Instead, it turns out that the notion of reliable electronic availability is alien to the brains of publishers who grew up with printed paper. The key point here is that the primary interest of authors is making their work widely available and, hopefully, recognized. But easy and permanent availability of articles is a domain mostly occupied by the open access movement, not by the publishing establishment.
Being an avid netizen I've long gained this impression that printed articles fade much faster into oblivion than articles published in an ad-hoc way. Let me just mention two examples. The late C/C++ Users Journal used to be a fine source of programming lore. But the links they printed in their articles already sucked when it was still bristling with buzz: They all read http://www.cuj.com/code as monotonously as the rattling of prayer wheels. For every article. This was not very useful. When they ceased to publish in 2006 and promised to feature more C/C++ topics in DDJ instead, even that link went dead although the old site was redirected to the new one. Preserving the entire domain should've been trivial. Right now, I'm greeted with the boring message “Sorry, the requested page is not found.” The second example is even more disturbing: On my writings page, I have linked a paper with a DOI. That DOI was advertised as being permanent when it was issued by the European Physical Journal (published by Springer) nine years ago. Here it is: 10.1007/s100529800947. It's been 404ing for many months now. At what point in time it stopped working, I cannot tell. In the meanwhile, the same article's arXiv.org link is still working fine and I even found a reference to that DOI on Springer's website. This rules out a typo as the reason for my not finding it. I've even contacted Springer five weeks ago but nothing is happening.
I am afraid, the publishers have completely failed to understand that they are not needed for issuing the blessing of peer reviewing which can be organized without them. Their paper editions are not needed either since most printing occurs on the laser printer down the hall or besides the desk. If, at the very minimum, they would care to organize permanent availability of the information! This way, search engines could do a better job indexing. The publishers would retain some of their attractiveness for authors and would serve everybody.
So, all you authors, scientific collaborations, and institutes: Don't prolong the agony! Do a big favor to all of us and publish your results online on web servers or –better even– upload them to a public e-print sever. If you are dead set on publishing your papers in a paper journal, just make sure you also publish it on an eprint server, too. Consider publishing in open access journals. Read the fine print of the copyright transfer and you'll generally see that you're entitled to put your papers online.
Update (10 October 2007):
Nine weeks after
filing a complaint, the DOI mentioned above has come life again.
Update (8 March 2019):
Removed link to the
C/C++ User Journal's website. Ironically, it has been hijacked by
ghouls.
4 September 2006
Spain is a country where time is a currency available in inflationary amounts. While attending the Second International Congress on Mathematical Software in Castro Urdiales, Cantabria, I was genuinely impressed by how relaxed people organize their day. The guy at the hotel lobby was irritated about me wanting a wake-up call at 8am. Breakfast? Not that early! I mostly went to lunch with fellow GiNaC hacker Chris Dams, Joris van der Hoeven, Torbjörn Granlund, and Niels Möller at about 1pm which was early compared to the Spanish folks. Nevertheless, at that time the bars were already overcrowded with folks having a glass of wine, a couple of cigarettes, and a heated conversation about the latest sports events. After dinner, everybody was hanging around in bars. And 11pm seems to be the perfect time for small children to play soccer on the town's plazas!
This was a good stay away from work with plenty of time to think about two main themes: First, floating-point arithmetic and the entire business of assessing output ranges of a computation. The more I think about it and talk to people, the more I'm becoming convinced that there is little point assessing the possibility of overflows, underflows, and other arithmetic problems in algorithms using PolySpace, Fluctuat, and other static tools. Effective dynamic error handling and recovery is much more important. And any modern FPU has built-in support for that, thanks to the wonderful IEEE-754 standard. Case in point: The first Ariane 5 was doomed before take-off due to bad static analysis. Maybe, doing better static analysis would have safed it at an exorbitant cost. But it would have been trivially safed by less brain-dead error handling. (Certain errors essentially shut the computers down.)
Second, on the computer mathematics front, there was a highly interesting session about formalizing proofs on the computer, organized by Freek Wiedijk. The intent of systems like HOL light, Coq, and Mizar is to be as small as possible and let the user derive theorems from a well-founded set of axioms. Basically, the user steers the machine from step to step by applying theorems with absolutely no chance of error. This is because every theorem he applies has itself been proven using the system. The point of having a small kernel is to make it entirely comprehensible for humans. It's impressive how even unwieldy theorems are formalized using such systems. While GiNaC is certainly not such a system, it is good to see that we agree on that point: Using GiNaC, one has to apply one method after another thus transforming terms and there is no miraculous “simplify” operation. In fact, we've always considered “simplify” as evil. I was carrying my laptop computer and, while traveling, had plenty of time playing around with Coq and HOL light. I must say that I like them. The only problem is: Although non-Spanish, their speed is not exactly impressive.
29 November 2005
Der erste Frost hat die Samtfußrüblinge aus den alten Baumstümpfen getrieben. Zeit, auf ein gutes und abwechslungsreiches Pilzjahr zurückzublicken.
4 October 2005
 |
The MPFR team is satisfied: Vincent Lefèvre, Paul Zimmermann, and Laurent Fousse. |
Sitting in the restaurant of an almost empty, ultramodern ICE train on my way back from the Many Digits Friendly Competition at Nijmegen I am musing about the results. First of all: in overall score, it appears clear that the MPFR team scored best, followed by myself with CLN/GiNaC, then iRRAM and several other ones (Mathematica, Maple, RealLib, FewDigits, Comp). Whatever that means.
 |
Yours truly, slightly overtired, running the solution programs. |
Not every system was able to run all the 24 problems: Originally, GiNaC/CLN couldn't do the root finding problem (C21) and the numerical integration problem C22. Therefore I had to go through some hacking sessions before arriving at Nijmegen. The worst joke was that I rewrote Romberg's integration method from the venerable Numerical Recipes in C for GiNaC/CLN and it even converged to 100 decimal digits precision within the two minutes timeframe! This is quite a success since, using Romberg's method, the effort grows superlinearly with the precision goal. Besides wild hacking and the quality of the systems, a factor eminently important to success or failure was how much effort the maintainers were willing and able to dedicate into meditating over the problems and finding clever solutions: It definitely helps throwing a bunch of really clever mathematicians at the problems and let them invent highly problem-specific solutions instead of generic code. The upshot was that the MPFR team was able to compute elements of the inverse of the 107×107 Hankel Matrix (hi,j=1/fib(i+j-1)). With GiNaC, I'm barely able to construct the 104×104 matrix and computing its inverse would take weeks. It's clear that they have found a closed formula but even Paul Zimmermann didn't know which one and appeared mildly surprised. Another clever thing to notice is that ∑n=1m1/n (problem C15) has something to do with the Digamma function ψ(m). Well spotted, but not really helpful until you have a way to compute that Digamma function ψ It turns out that an asymptotic expansion for large m was enough and Norbert Müller of iRRAM and Paul Zimmermann really did implement it. Another opportunity of creative hacking was problem C19: it converged extremely fast for all systems but that was a red herring! If you observe that the result can be written down without computing in base 7 and all that remains to be done is a conversion to base 10, you'll win the day. Paul Zimmerman did observe. And he, well, won the day.
 |
The competitors studying the results. |
The pictures show some of the contestants drinking beer and studying the preliminary results published after the competition was almost over. The competition itself was a rather silent event that took place during the TYPES workshop. They led each of us (or each team) in turn to a computer where we would run the problems. Milad Niqui and Freek Wiedijk were taking extreme care that the programs were not disturbed in any way. They even went so far and rebooted the machine before each system's turn! After measuring the timings, the results were immediately checked for correctness. Each of us was given an hour time. If all goes okay, an hour is plenty. But if anything goes wrong, an hour is not much time for fixing things. I was lucky and had no problems. I had some headache before my turn, though, due to some misunderstandings of the problems. For instance: what is 666? Is it (66)6 or really the much, much larger 6(66)? It turned out to be the latter.
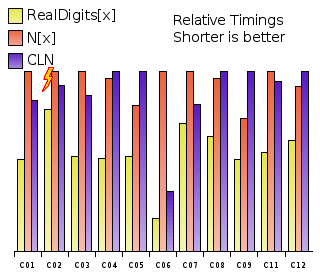
|
|
Mathematica 5.2 is about as fast as CLN when
used naively. Using RealDigits and converting to a number with FromDigits
instead of just computing the number with N, it is suddenly much
faster. Why?
|
What really irritated (or even shocked) all of us was the entry of the Wolfram Research Team. They didn't even try to run the more complicated problems where some programming effort was needed. But in the basic problems their timings shined and they scored best in most of them, beating even CLN. This surprised me so much I had to do some little experiments of my own. First result: The Mathematica kernel has gained a lot of efficiency over the last few releases when it comes to numerics. (The current release and the version they used at the competition is 5.2). Since all problems were dealing with trigonometric functions it is unlikely that this efficiency is due to the libgmp.so.3 sitting in the Mathematica tree. Second result: It's impossible to get to such timings with naively applying the N[f(x), Digits] command for numerical evaluation. So, how else then, did they do their computations? One has to look at their solutions to find out. The first problem C01 was to compute sin(tan(cos(1))) and they computed it to 105 decimal digits. But, instead of N[Sin[Tan[Cos[1]]],100000] their script looks basically like this: $MaxExtraPrecision = 100000 FromDigits[Take[First[RealDigits[Mod[Sin[Tan[Cos[1]]], 1], 10, 100010, -1]], -10]] Though this will print only the last 10 digits, changing the last parameter to -100000 in order to print the entire fractional part does not change the timing substantially. On average, this way of computing the fractional part turns out to be twice as fast! The yellow bars are the timings I obtain with the solutions as formulated by the Wolfram Research Team, the red bars are the timings I obtain with with N[f(x), Digits]. For comparison, I've added the CLN timings (blue bars) and normalized them all such that the tallest bar always has the same height. Playing around with their scripts I can assert that this is a genuine speedup that comes from the RealDigits function, not from the Mod[,1] or anything else there.
What could possibly be going on there? Is there a way to print the digits in base 10 faster than by actually computing the number? Not unless the computing is inefficient because one could always base the computation on evaluating the decimal digits! So what we are seeing may just be some quirk within the Mathematica kernel. If you have only the slightest idea how the RealDigits function can give a speedup, please let me know.
Notice that I've omitted problem C10 from the graph. I did this, because there is only one data point for Mathematica, not two: The Wolfram Research Team did not use the RealDigits bypass here. I tried it: it consistently bails out with an Floor::meprec: Internal precision limit $MaxExtraPrecision reached error even if I crank up $MaxExtraPrecision to 107. Also very interesting is the fact that due to the rules of the competition, CLN won the C02 problem. This is because Mathematica 5.2 miscomputes the last 53 decimal digits! This miscomputation did not happen with Mathematica 5.0, it started with 5.1. Curiously, it happens also when the naive way N[Sqrt[E/Pi],1000000] is employed. There, it even happens 5 decimal digits earlier. Anyways, why the Wolfram Research Team hasn't even tried the second half of the problems and instead chose to show off some voodoo tricks remains a mystery. They could have scored better.
Update (12 November 2005):
Fellow competitor Vincent Lefèvre emailed me
regarding the speculations about the Mathematica “anomaly”.
He found that the Mathematica book mentions in Section
A.9.4 that RealDigits uses a recursive divide-and-conquer
algorithm while N adaptively increases the internal working
precision. Still, how that can account for a factor 6 difference in
performance for the relatively simple problem C06 (compute
atanh(1-atanh(1-atanh(1-atanh(1/Pi))))) is beyond me.
Update (20 July 2006):
Ed Pegg Jr. of Wolfram
Research wrote an email explaining the reason why they didn't try all the
problems: He had to support a “huge technology conference at the
time” and he had no help from anyone else. I tried asking him about the
point of having N and RealDigits be based on entirely
different algorithms, but haven't received an answer. Maybe, they don't know
either.
 |
Die Gipfelstürmer Cebix, Marc und Natan |
29 Mai 2005
Marc H. war da. Besser gesagt, er war bei Cebix. Wir nahmen Natan mit und starteten zu einer Herrentour durch die Fränkische Schweiz, wo wir zunächst einmal den Rötelfelsen bezwangen: nicht wie gewöhnliche Bergsteiger immer über den kürzesten Weg, nein, die wagemutigen Recken rechts im Bild bevorzugten den mühevollen Umweg um die Felswand herum durch finsteren, gefahrenvollen Wald.
Dem Zusammenbruch nahe, überstieg das Ausmaß des Durstes deutlich dasjenige der Maßkrüge hinterher im Lindenkeller. Danach ging's dann noch hinauf auf das Walberla und zum “Dennerschwarz”. Trotz unterschiedlicher Trinkgewohnheiten haben sich Natan und Marc prima verstanden. Ich glaube ich kann Natan mal ein paar Tage ausleihen. Hi Marc! ;-)
10 September 2004
This year's Linux Kongress ended today. As it took place over here in Erlangen (again) I had to be there. My tiny place was mildly crowded, with Cebix and Michael H. staying here. Much fun was had. The Kongress was mixed, as always, with some very good talks, some very bad talks and some surprises. I didn't even know that Linux can do snapshots on the block device layer! If you think you know something about Linux and you have not seen any of Jos Visser's Komplete Konfusion Kuiz, then you might not even know how wrong you are. Also, Ted Ts'o was there, as always. He's the bone-crushing Sumo of Jos' hilarious show. He can fluently read (and understand) /etc/sendmail.cf files that anybody else uses only to initialize their entropy pools!
17 October 2003
Just returned from the Linux-Kongress in Saarbrücken where I went together with Michael H. We stayed at Jörg K.'s place and had a lot of fun (and, perhaps, too much beer). Smart cards and such security devices seem to be on everyone's mind, nowadays.
15 October 2002
I've left ThEP to start working at Framtome ANP in Erlangen as a full time software developer contributing to the Teleperm XS digital I&C system. Yes, I'm still using free software at work. Linux, Emacs, GCC, you name it. Oh, and thank you very much for asking. ;-)
25 May 2002
Having just returned from the first Workshop on Open Source Computer Algebra, I'm musing about what the future will bring to us with regard to open source CAS. On the surface, the computer scientists have more inclination to really integrate their systems than the physicists in Tokyo had. I'm not sure if that will help us, though. Apparently, when you put 20 or so of them in one room to work on one project, then what comes out is a specification of a system that has to have 20 great pet features but lacks a clear vision. Also, in the unlikely event that they eventually start writing code, they will soon face the problem of interfacing 20 languages, because everyone is convinced about the superiority of his language. Oh, well.
I wouldn't say all is lost, though. It was good to learn that the Axiom sources are in the process of being polished for release under an open source license. We can all look forward to Tim Daly publishing them soon. Also, Joris van der Hoeven has done a terrific job with TeXmacs. It shouldn't be too difficult integrating GiNaC into it.
8 April 2002
Finally handed in my PhD thesis, just in time before the esteemed visitor arrives. In order to avoid hard copies or microfilm, I decided to go the electronic way. But then the morons at the Mainz University library insisted on removing all pixelized Type 3 fonts from the PDF document because they look ugly when viewed with Adobe's Acroread. This is silly, however, because there is nothing wrong with the fonts per se, rather with the way Adobe's product renders them. When printed or viewed with ghostscript or xpdf you don't see any difference at all between Type 1 and Type 3. What kind of reference implementation is this? Luckily, I was able to find Jörg Knappen's fine EC fonts as Type 1 on a russian FTP server. It took me an entire week to massage the LaTeX but the result looks good even in acroread. It's amazing how the brave new world of digital publishing sucks big time.
5 December 2001
 |
Talking about physics? |
Returned from Tokyo, where the CPP2001 Workshop took place. The picture on the right was taken at the workshop. Apparently, I am talking about computational physics and have arrived at my last slide. One of the most disturbing appearances was Fyodor Tkachov, who not only seriously advocated the use of Oberon in high energy physics computation but also spread some confused and misleading information about other languages, especially about C++. At one point he seemed to suggest to rewrite the entire Root framework from scratch in Oberon! Eventually, all this turned rather ridiculous as it became apparent that Fyodor picked a fight with everyone who chose to do things in a different way. Jos Vermaseren seemed to be one of his favored targets, which is okay, since Jos is clever enough to defend himself from this kind of attacks. Thorsten Ohl was there, too, evangelizing functional programming languages, especially O'Caml. Everybody seems to have his own pet system and little inclination to interface with others and build something really useful. For these people, to interface seems to mean to rip informal textual output from one package and unsystematically stuff it into another one.
A somewhat disappointing experience was a session in which Jos Vermaseren tried to figure out what high energy physicists are most missing from the computer algebra systems Form and GiNaC. It was supposed to be a good opportunity to complain because the authors of the two systems were present and listening. Some people did complain. Two or three people picked on Form not simplifying tensors cleverly enough automatically. The complaints did not appear to be well-founded, however, since what we implementors need are clear-cut algorithms, not demands to perform some kind of magic. What can we learn from this? For me, it is obvious: if you have a clear and pristine vision what ought to be done, then, for heaven's sake, do it! Pay attention to your customers when they approach you with suggestions how this or that detail might be helpful in practice. But refrain from querying them what they want, because in most cases they have neither a clear understanding how the machine works, nor a clear idea what it is they actually expect from it.
On the brighter side, I met Elise de Doncker of Western Michigan University. It was good to learn that some mathematicians are really caring about numerical integration of ill-behaved integrands and maintain good implementations like ParInt. Methinks the time has come to finally ditch the venerable Vegas algorithm.
The conference featured the best conference dinner I've ever had: 10 courses of Japanese delicacies in a traditional Japanese restaurant-temple called “Ukai-Chiku-Tei” in Takao. After the dinner came the revelation: the whitish piece of fish during the third or fourth course was actually fugu, that pufferfish that can be lethally poisonous if prepared by inexperienced chefs. I may have thought that this seafood's exorbitant price tag must be accompanied by an exceptional taste. Now, I am freed from this fallacy. Well, it's not bad, but what makes this dish interesting is certainly the assumed risk, not some exotic savor.
Christian Bauer was the official chronicler of that journey. I heartily recommend his terrific account. Japan is a vibrant country, both ultramodern and highly traditional. I've only been there for about a week and not even left Tokyo metropolitan area, but even so, the impression was overwhelming and I wish, I can come back soon.
20 October 2000
The ACAT 2000 workshop at Fermilab is finally over. Apart from some inspiring talks with Bjarne Stroustrup about what's good and bad about C++, the most memorable experience was meeting Jos Vermaseren of Form fame. He's a very nice fellow and genuinely interested in our work on GiNaC. The first few days I couldn't resist pulling his leg about Form being commercial software. Then came the surprise: he announced Form 3 as being available for free (as in beer) and mentioned that he would be interested in making Form really open source, once some obscure corners have been cleaned up.
21 March 1998
 |
At the TRACS flat (Santiago, stop laughing, please!) |
To the dismay of all the nice people who came to yesterday's dinner party, I've brought a luggagefull of genuine Scottish haggis from winterly Scotland where I spent the last eight weeks at the Edinburgh Parallel Computing Centre EPCC. The stay was supposed to serve the purpose of porting pvegas, my parallel version of Lepage's vegas algorithm to those really big machines that cannot be programmed under some thread paradigm but instead sport some sort of message passing. Like the Cray T3D/T3E. Well, two months is a lot of time for porting a program of less than 1kLOC, but still, it's only almost finished. (I think it works correctly now, but I still need to do some thorough testing, polish it up, do some final benchmarking, and test it on a loosely coupled network of workstations.) The lesson I've learned is that you can't just port a piece of code from a SMP environment to one based on message passing. You rewrite it. You turn it's entire structure inside-out. And, of course, you re-debug it. The two worlds just cannot be bridged with a couple of cleverly placed #defines here and there.
 |
Gavin and Stefan are responsible for the constant shortage of salt at the TRACS flat. |
Anyway, this little expedition has been extraordinarily instructive. At the EPCC, they teach their visitors a course of something interesting about once a week. And what they do is not some lame stuff like how to do parallel software builds using GNU make, but almost always something surprising. Besides being instructive, the expedition has also been hilarious. Like most people on a research stay to the EPCC, I've been living at the TRACS flat on the University's King's Buildings campus. When you cram half a dozen people from all over Europe into a flat, fun just can't be avoided. We went dancing at a couple of traditional Scottish cèilidhs, rented a car to drive to the Isle of Skye off the gusty Scottish west coast, danced to the wild tunes of The Prodigals at the Finnegan's Wake Irish bar, had dozens of dinner parties with folks from the EPCC, and generally enough wine, beer, and single malt whisky.
One unforeseen distraction I had has been the discovery of a very revealing file named bi.tar sitting right inside the /root/ directory of one of the Linux machines I'm administering in Mainz. We've had an anomaly on new year's eve, where one of our user accounts seemed to have been compromised. It wasn't entirely clear, however, whether somebody just got access to the account by watching him type the password or something similar. Anyway, that file bi.tar file contained a binary of the juggernaut TCP connection hijacking program and C source file that was apparently supposed to clear entries from the wtmp login record file. Looking around further, I discovered that the file /root/.bash_history was most interesting: The cracker must have tried to blur his traces by even removing root's .bash_history, but apparently was not aware of the fact that GNU bash writes out its history in one go when exiting! This way, when you remove the file, you really only remove the older logs. D'oh! It suddenly all made sense: the cracker has been able to take over control because he had physical access to the machine: A number of reboots have left their traces in the log files. He has harvested passwords by listening to network traffic and transferred the harvest via ftp to his lair machine. Now, it was easily guessed who the guy was and the people in Mainz were informed in order to stop this. This was an uneasy experience: I wish it had not happened or that it had been somebody else.
Over all this hacking I've hardly been doing any physics during this stay. I shared an office with some other folks at the physics building and our office was right opposite the office of Peter Higgs, yes, the very Peter Higgs of Higgs boson fame. The remarkable thing about this is that I didn't get to see him. Not even once. Even though I was supposed to be very close to the threshold of production! Consequently, I've come to be sceptical about the Higgs particle itself. Maybe it doesn't exist. Maybe this is a big hoax and neither Professor Higgs nor his particle exist at all? This is soo spooky.